

If the boat holds 2 people, then 2 couples require 5 trips with 4 or more couples, the problem has no solution. not in the presence of any men on the shore), then this puzzle can be solved in 9 one-way trips:Īn obvious generalization is to vary the number of jealous couples (or missionaries and cannibals), the capacity of the boat, or both. If a woman in the boat at the shore (but not on the shore) counts as being by herself (i.e. The solution just given is still shortest, and is one of four shortest solutions. In this case we may neglect the individual identities of the missionaries and cannibals.
If however, only one man can get out of the boat at a time and husbands must be on the shore to count as with his wife as opposed to just being in the boat at the shore: move 5 to 6 is impossible, for as soon as γ has stepped out b on the shore won't be with her husband, despite him being just in the boat.Īs mentioned previously, this solution to the jealous husbands problem will become a solution to the missionaries and cannibals problem upon replacing men by missionaries and women by cannibals. This is a shortest solution to the problem, but is not the only shortest solution.

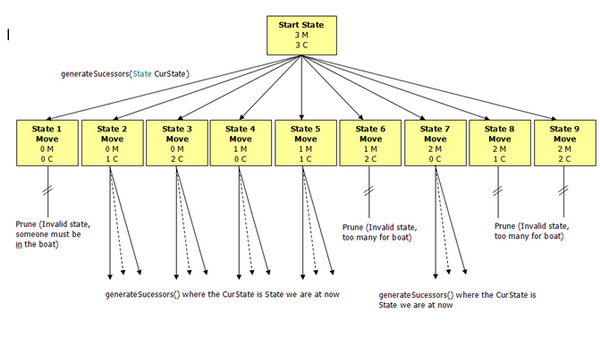
In the right figure, if a wife or cannibal staying on the boat counts as being by herself (circled), a shorter solution is possible. The solid red line optionally denotes the cannibal unable to row. Timeline solutions to both jealous husbands, and missionaries and cannibals problems, with the vertical axis denoting time, blue denoting husbands or missionaries, red denoting wives or cannibals, yellow denoting the boat, and lines of the same type denoting married couples (in the jealous husbands problem). The married couples are represented as α (male) and a (female), β and b, and γ and c. The earliest solution known to the jealous husbands problem, using 11 one-way trips, is as follows. This is the goal state, and the path from the root of the tree to this node represents a sequence of actions that solves the problem. The algorithm continues alternating subtraction and addition for each level of the tree until a node is generated with the vector ⟨0,0,0⟩ as its value. For each of these remaining nodes, children nodes are generated by adding each of the possible action vectors. Any node that has more cannibals than missionaries on either bank is in an invalid state, and is therefore removed from further consideration. The five possible actions (⟨1,0,1⟩, ⟨2,0,1⟩, ⟨0,1,1⟩, ⟨0,2,1⟩, and ⟨1,1,1⟩) are then subtracted from the initial state, with the result forming children nodes of the root. To fully solve the problem, a simple tree is formed with the initial state as the root. The state would reflect that there are still three missionaries and two cannibals on the wrong side, and that the boat is now on the opposite bank. For instance, if a lone cannibal crossed the river, the vector ⟨0,1,1⟩ would be subtracted from the state to yield ⟨3,2,0⟩. Actions are represented using vector subtraction/addition to manipulate the state vector. Since the boat and all of the missionaries and cannibals start on the wrong side, the vector is initialized to ⟨3,3,1⟩. The vector's elements represent the number of missionaries, cannibals, and whether the boat is on the wrong side, respectively. Solving Ī system for solving the Missionaries and Cannibals problem whereby the current state is represented by a simple vector ⟨m, c, b⟩. Therefore, upon changing men to missionaries and women to cannibals, any solution to the jealous husbands problem will also become a solution to the missionaries and cannibals problem. Under this constraint, there cannot be both women and men present on a bank with women outnumbering men, since if there were, these women would be without their husbands. In the jealous husbands problem, the missionaries and cannibals become three married couples, with the constraint that no woman can be in the presence of another man unless her husband is also present. And, in some variations, one of the cannibals has only one arm and cannot row. The boat cannot cross the river by itself with no people on board. In the missionaries and cannibals problem, three missionaries and three cannibals must cross a river using a boat which can carry at most two people, under the constraint that, for both banks, if there are missionaries present on the bank, they cannot be outnumbered by cannibals (if they were, the cannibals would eat the missionaries).


 0 kommentar(er)
0 kommentar(er)
